Water drop 3a – Physically based wet surfaces
March 19, 2013 9 Comments
Version : 1.3 – Living blog – First version was 19 March 2013
This is the third post of a series about simulating rain and its effect on the world in game. As it is a pretty big post, I split it in two parts A and B:
Water drop 1 – Observe rainy world
Water drop 2a – Dynamic rain and its effects
Water drop 2b – Dynamic rain and its effects
Water drop 3a – Physically based wet surfaces
Water drop 3b – Physically based wet surfaces
Water drop 4a – Reflecting wet world
Water drop 4b – Reflecting wet world
Physically based rendering (PBR) is now common in game (See Adopting a physically based shading model to know more about it). When I introduce PBR in my company few years ago we were actually working on rain. At this time we were questioning about how our new lighting model should behave to simulate wet surfaces. With classic game lighting model, the way everybody chose was to darken the diffuse term and boost the specular term (Here I refer to the classic specular use as RGB color to multiply with the lighting). The wet diffuse/specular factors being eye calibrate. I wanted to go further than simply adapt this behavior to PBR and this required to better understand the interaction between water and materials. This post is a mix of the result of old and recent researches. I chose to provide up to date information including experimental (not complete) work because the subject is complex and talking about it is useful. This might be of interest for future research. The post describe how water influence materials and provide ways to simulate wet surfaces with physically based lighting model. I suppose here that’s the reader know the basics of reflected/refracted lights with Snell’s law and index of refraction (IOR).
Wet surfaces – Theory
People are able to distinguish between a wet and a dry surface by sight. The observation post show many pictures to illustrate this point. The main visual cue people retain is that wet surfaces look darker, more specular and exhibit subtle changes in saturation and hue when wet:
This behavior is commonly observed for natural or human made rough material/porous materials (brick, clay, plaster, concrete, asphalt, wood, rust, cardboard, stone…), powdered materials (sand, dirt, soil…), absorbent materials (paper, cotton, fabrics…) or organic materials (fur, hair…). However this is not always the case, smooth materials (glass, marble, plastic, metal, painted surface, polished surface…) don’t change. For example, there is a big difference between a dry rough stone and a wet rough stone but a very small difference between highly polished wet stone and highly polished dry stone.
In the following discussion, wet surfaces refer mostly to rough and diffuse materials quenched in water and having a very thin water layer on their surfaces.
Why rough wet surfaces are darker when wet ? Because they reflect less light.
There is two optical phenomena imply in this decrease of light reflection and they are details in [3] and [4]. A rough material has small air gaps or pores which will be filling by water when wetting process begin. When pores are filled, there is “water saturation”, water propagates onto the material as a thin layer.
Let’s first see the impact of the thin layer of water. The rough surface leads to a diffuse reflection (Lambertian surface). Some of the light reflected from the surface will be reflected back to the surface by the water-air interface due to total internal reflection. Total internal reflection occur when moving from a denser medium into a less dense one (i.e., n1 > n2), above an incidence angle known as the critical angle (See [1] for more detail). For water-air interface, this is
This reflected light from the surface is then subject to another round of absorption by the surface before it is reflected again. This light’s back and forth result in darkening of the surface.
Now take a look at the water filling in the pore inside the rough material. There is a concentration of water beneath the surface. The water which replace the air have an index of refraction higher than that of air (1.33 against 1.0) which is closer to index of refraction of most rough dielectric material (1.5). Consequence, following the Snell’s law, light entering in material will be less refracted due to the reduced index of refraction difference: The scattering of light under the surface is more directional in the forward direction. The increase scattering events before the light leave the surface increases the amount of light absorbed and thus reduce the light reflection.
The darkening of the material is also accompanied by a subtle change in saturation and hue. In [11] the spectral reflectance (i.e the “RGB” representation of real world color, the visible range of the spectrum is around 400nm blue to 780 nm red) of a dry and wet stone has been measured to highlight these characteristics. Analyze show that’s there is a significant reduction in reflectance across the whole range of the visible spectrum when the surface gets wet. Which confirm the darkening of the surface. It also show that’s the surface color becomes more saturated because of this reduction.
Source [11].
There is also a good plain word explanation in [13]:
More internal reflections accentuate the effect of spectral variations and results in changes in hue and saturation. That is, if a material reflects long “red” wavelengths more than short “blue” wavelengths, the reflected distribution of light after two reflections has a greater percentage of energy in the long wavelengths than the short, and will appear to have shifted in hue and have a more saturated color.
Why rough wet surfaces are more specular ? The air gaps of the rough surface are progressively filled with water and water has almost a mirror-like behavior. The rough surface leads to a diffuse reflection which is progressively replaced by a specular reflection due to water. In simple word, the material becomes smoother. A polished, a coated or a wet stone are similar smooth surfaces.
In the case of a smooth material, the water doesn’t fill inside the material and do not produce darkening from within the material. But the darkening from the thin layer of water still happens as describe for the reflected light of the surface above.
From a rendering point of view, we should take care of both optical phenomena: the one due to a layer of water on the surface and the other considering water inside the material. A two-layer surfaces reflection and subsurface scattering lighting model is presented in [2] by Jensen and al. The surface model is a thin layer model, with a thin layer of water between the external air and the denser material. The dense material is modeled as scattering volume. Note that’s their handling of the subsurface scattering allow the rendering of the increased translucency of thin materials caused by the absorption of the water (like paper, cloth…). In this post we will not consider these kinds of materials.
This Jensen et al.’s lighting model is too expensive to be use in real time. To study what can be done in the context of game, we will consider the two optical phenomena separately. The following will describe a lighting model for the thin layer of water on top of smooth and non porous surfaces, then a lighting model for the interaction inside a porous material. After what we will try to extract something useful for game (which will be detailed in the b part of this post).
Realtime double layer material
To simulate the presence of a thin layer of water above a surface, we need to have a double layer BRDF, the top layer BRDF will be the water and the bottom the original BRDF. One usable real time implementation which can be adapted for our case is the model from Weidlich and Wilkie [19][20][21].
Weidlich and Wilkie present a layered BRDF allowing combining several micro-facets BRDF into a single unified and accounting for both internal reflection and absorption. Each layer can have any arbitrary BRDF. Their approximation supposes that layers are thin in comparison with the surface geometric which is the case for our thin layer of water on top of material but not a puddle.
Here is a sum up of their process (For a detailed explanation, reader should refer to the paper):
1. The BRDF of the topmost level fr1 is evaluated for the two given, arbitrary incoming directions wi, and wo. This yields a reflection component, and, except at the lowest layer, two refraction directions.
2. Any energy that is refracted into the next level T12 follows the two refraction directions associated with the initial incident directions, and is partly absorbed a by the medium.
3. These two refraction directions are assumed to meet at a single point on the next layer fr2 , and the process is repeated from step 1 until an opaque layer without a refraction component is encountered.
4. On returning from the recursion, the individual BRDF components are attenuated by the Fresnel transmission coefficients T21 for the level above them, and added to the total BRDF.Source [19]
This is formulate as follow:
with the absorption term.
and
are the refracted angle.
The absorption inside a transparent material follows the Bouguer-Lambert-Beer law. is a wavelength dependent absorption coefficient and
is the thickness of the layer. The term
represent the distance travelled back and forth by the light in the layer. According to this law, internal absorbance, and thus the corresponding colour, increases with the travelled distance. As a consequence the colour decreases and the saturation increases, but additionally it can change the hue. The thickness should be providing in the inverse length unit of the absorption coefficient. For example, if the absorption is 0.35 by meter, the thickness should be providing in meter. If it is 0.0035 by centimeter, the thickness should be in centimeter.
try to handle the case of total internal reflection interaction in the layer and is defining as (refer to [20] for more details) :
is here to accounts for the energy that is not able to immediately leave the medium.
Note that can be rewrite
A full implementation of this model is provided for renderman shading language in [21] ([20] have also some part of it). A minimalist implementation is providing for pbrt-2 in [10] with an extension to a generalized version. A real time implementation targeting GPU is also available in [12]. However the GPU implementation lacks some part of the original implementation like environment map for second layer.
Before beginning with this model I should advice that’s the paper is not verbose enough for starter with its model. There is missing information on the input of and
term to uses and in fact it differ between the implementations. It appear that’s
and
should use the refracted vector, in the GPU implementation it use top layer vector.
is also based on the top layer. Moreover, depend on the implementation, the calculation of the refracted vector is done with the normal N or with the half vector H (If someone will to explain me the why of this ?) and this can result in different analyze (see the added note of this post). In case of using the half angle to refract ray, the refracted half vector H’ is opposite to the original half vector H. Here I chose to follow the implementation provide in [21] by the authors.
We can adapt this layered BRDF for our double layer BRDF. The top layer will be water. As our top layer is a perfect specular water should be 1 and
become
.
Our double layer BRDF is now:
I have implemented this BRDF to better study it. For this, I wanted to used the real absorption coefficient of the water. The absoprtion spectrum of pure water can be found in [22], the unit is . I gather the values in one text file if anyone is interested: AbsorptionSpectrumPureWater (Right click, save as… Rename file from “.pdf” to “.txt”. Necessary step as WordPress doesn’t support txt file). Integrating this spectrum against the CIE color matching function and converting it to RGB give:
This absorption coefficient mean that’s at 1 meter under pure water (so not the exact real value of water like in the sea but not too far), your red light component is attenuated by . So you get 70% of the original red light component. So we see that’s red light is the first to be absorbed then green light then blue light (in reality blue absorption is not 0 but really small). For this post, I chose centimeter as unit for thickness, so
Here is an example image for a simple dielectric ground. Left is dry ground, second is is wet ground with a thickness of 0, third is wet ground with a thickness 0.5 (which mean 0.5mm in this context), right is wet ground with a thickness of 50 (i.e 50cm in this context). There is an analytic point light not visible at top middle of the image, far in the background.
I tune the thickness component in the absorption term to 50cm to highlight the impact of the aborption on the darkening of the color. But such a value, of course, don’t match the reality of a thin layer of water and won’t be discuss.First thing: Thockness 0 and thickness 0.5 are almost identical highlighintg that the absorption for this double layer BRDF in the context of thin layer of water is negligible. Second, we can see that’s there is a small change in specular and a really slight change in diffuse reflections between the dry and wet (thickness 0.5) ground. The change of diffuse reflection is because less light reach the ground.
Here is another example with a middle rough copper metal ground (No diffuse), same settings. The color comes only from the environment:
Again, in case of metal, we have a slight change in specular reflection, more smooth for the highlight and less bright for other part.
I have implemented this BRDF in AMD RenderMonkey if you want to play with it. I made a zip file containing the RM project, the textures and the ground mesh. As WordPress don’t support zip file, I rename the zip in pdf. So to download the application right click on the following link : Rendermonkey-double-layer3, save target as… and then change the extension to “.zip”. You can switch from metal or not with define. I chose to implement the accurate version with true Fresnel formula to highlight the features of this BRDF. Here is the main part which is a straight implementation based on the code in [21], comment in the code should be sufficient to get it:
// Eta is relative IOR : N2/N1 with to / From
// CosTheta is dotVH
float FullFresnel(float Eta, float CosTheta)
{
float c = CosTheta;
float temp = Eta* Eta + c * c - 1;
if (temp < 0)
return 1;
float g = sqrt(temp);
return 0.5 * Square((g - c) / (g + c)) *
(1 + Square(( (g + c) * c - 1) / ((g - c) * c + 1)));
}
// FresnelConductor Exact
float3 FresnelConductor(float3 I, float3 N, float N1, float3 N2, float3 K)
{
float3 Eta = N2 / N1;
float3 Etak = K / N1;
float3 CosTheta = dot(N, I);
float CosTheta2 = CosTheta * CosTheta;
float SinTheta2 = 1 - CosTheta2;
float3 Eta2 = Eta * Eta;
float3 Etak2 = Etak * Etak;
float3 t0 = Eta2 - Etak2 - SinTheta2;
float3 a2plusb2 = sqrt(t0 * t0 + 4 * Eta2 * Etak2);
float3 t1 = a2plusb2 + CosTheta2;
float3 a = sqrt(0.5f * (a2plusb2 + t0));
float3 t2 = 2 * a * CosTheta;
float3 Rs = (t1 - t2) / (t1 + t2);
float3 t3 = CosTheta2 * a2plusb2 + SinTheta2 * SinTheta2;
float3 t4 = t2 * SinTheta2;
float3 Rp = Rs * (t3 - t4) / (t3 + t4);
return 0.5f * (Rp + Rs);
}
(...)
// Model from Weidlich and Wilkie
// Top layer : Water layer - Fr1
// Precalc values for lighting equation
float3 V1 = normalize(Input.ViewDir);
float3 L1 = normalize(LightPosition - Input.Pos);
float3 H1 = normalize(L1 + V1);
float dotVH1 = saturate(dot(V1, H1));
float dotNH1 = saturate(dot(N, H1));
float dotNL1 = saturate(dot(N, L1));
float dotNV1 = saturate(dot(N, V1));
// IOR of water is 1.33 or 0.02 at normal incident
float F12 = FullFresnel(1.33, dotVH1);
float T12 = 1 - F12;
// Simulate a mirror-like reflection for water
float Fr1 = F12 * ((200 + 2.0) / 8.0) * pow(dotNH1, 200);
// Indirect lighting contribution
float3 R1 = reflect(V1, N);
float F12CubeMap = FullFresnel(1.33, dotNV1);
// Perfect gloss of 1.0 for water
float3 Env1 = F12CubeMap * SampleEnvmap(R1, 1.0, Input.Pos);
// Second layer : Dielectric of IOR 1.5 - fr2
// Calculate refracted ray - reverse to be outward from center of second layer
float3 L2 = refract(-L1, -H1, 1.0 / 1.33);
float3 V2 = refract(-V1, -H1, 1.0 / 1.33);
float3 T21 = 1.0 - FullFresnel(1 / 1.33, dot(V2, H1));
float3 H2 = normalize(V2 + L2);
// Precalc values for lighting equation
float dotVH2 = saturate(dot(V2, H2));
float dotNH2 = saturate(dot(N, H2));
float dotNL2 = saturate(dot(N, L2));
float dotNV2 = saturate(dot(N, V2));
// Convert Gloss [0..1] to SpecularPower [0..2048]
float SpecPower = exp2(Gloss * 11);
#if METAL
// Copper n and k value are calculated from the spectrum data of the company filmetrics
// by convolving with the color matching function.
float3 F23 = FresnelConductor(V2, H2, 1.33,
float3(3.406149, 2.161600, 1.504326),
float3(5.225178, 3.756258, 3.018729));
float3 Fr2 = BaseDiffuse + F23 * ((SpecPower + 2.0) / 8.0) * pow(dotNH2, SpecPower);
// Indirect lighting contribution (code derive from Weidlich and Wilkie)
float3 F23CubeMap = FresnelConductor(N, V1, 1.33, float3(3.406149, 2.161600, 1.504326),
float3(5.225178, 3.756258, 3.018729));
float3 Env2 = F23CubeMap * SampleEnvmap(R1, Gloss, Input.Pos); // Reuse same R1
#else
float F23 = FullFresnel(1.5 / 1.33, dot(V2, H2));
float3 Fr2 = BaseDiffuse + F23 * ((SpecPower + 2.0) / 8.0) * pow(dotNH2, SpecPower);
// Indirect lighting contribution (code derive from Weidlich and Wilkie)
// We may use the refracted V for Fresnel but stay with the original code which use V.
float3 F23CubeMap = FullFresnel(1.5 / 1.33, dotNV1);
// The environment reflection must take into account the upper layer roughness,
// in Weidlich and Wilkie they use (m_base + m), so they add roughness of top layer to the one
// of bottom layer. As we deal with mirror-like specular for top layer, we don't do anything.
float3 Env2 = F23CubeMap * SampleEnvmap(R1, Gloss, Input.Pos); // Reuse same R1
#endif
// Absorption of water is float3(0.35, 0.04, 0.0) by meter
float Dist = Thickness * (1.0 / max(0.001, dotNV2) + 1.0 / max(0.001, dotNL2));
float Absorption = exp(-float3(0.0035, 0.0004, 0.0) * Dist);
float3 Fr = Fr1 + T12 * Fr2 * Absorption * T21;
float3 FinalColor = LightIntensity * (Fr) * dotNL1 + Env1 +
Env2 * T12 * Absorption * T21;
(...)
Note that’s the normal N use in this model is the one from the normal map of the ground. The thin layer of water in this case is not totally flat. I chose to follow the original implementation of Weidlich and Wilkie but this doesn’t sound an unreasonable choice.
This double layer BRDF seems to do part of the job expected for wet surface. Slight darkening of the underlying diffuse reflection, Fresnel reflection on the top layer. This model in itself is not sufficient to get the look we want for a wet surfaces, or at least it is not sufficient if we stay in reasonable value of “Thickness” for the layer. Moreover, in its current state, this code is too expansive and simplification need to be perform to be usable. The following will discuss some optimizations and problems related to game development of this double layer BRDF. I will often refer to the work of Tri-Ace presented by Yoshiharu Gotanda in [6] as they provide several optimization for the original Weidlich and Wilkie model. There will also be plenty of graph next, and all are available in a Mathematica file at the end of this section.
Refract vector
It seems that’s Tri-ace for the sake of simplification doesn’t handle refracted vector at all. I haven’t check the consequence of this choice but the origin of this decision come mainly from the cost of the refract code. As we deal about a layer of water, we could perform some optimization here. The original form of refract is:
float3 refract( float3 i, float3 n, float eta )
{
float cosi = dot(-i, n);
float cost2 = 1.0f - eta * eta * (1.0f - cosi*cosi);
float3 t = eta*i + ((eta*cosi - sqrt(abs(cost2))) * n);
return t * (float3)(cost2 > 0);
}
This is 11 instructions and consumes around 6 cycles on a PS3. As we need two refracted vector, we get 22 instructions and around 9 cycles (The PS3 compiler is able to perform some scheduling of instruction here).
With the knowledge that’s we refract through a air-water interface (mean a eta of 1/1.33), so we are not subject to total internal reflection, we can try to optimize a part of the refract code. A FindFit approach with Mathematica allow to approximate “eta * cosi – sqrt(abs(cost2))” (blue) by a polynome of order 2 :
-0.666308423880957 + 0.7518796992481197 X – 0.34853799144237796 X^2 (red):
A normalize is not needed but could correct a little the already good approximation. Converting polynome to Horner’s form and inject all this in original refract code we get:
// Refraction fine-tuned for eta = 1/1.33
// this work because we go from a lower IOR to
// a higher IOR so no total internal reflection
float3 refract_1_33(float3 i, float3 n)
{
float4 C = float4(0.75187969924, -0.666308423880957,
0.7518796992481197, -0.34853799144237796);
float cosi = dot(-i, n);
return C.x * i + ((C.w * cosi + C.z) * cosi + C.y) * n;
}
Thank to Sam Hocevar for the help provide to optimize this code. The code is now 5 instruction: 1 dot, 3 mad and 1 mul and around 3 cycles on PS3. The doubling cause 10 instruction and around 6 cycles (But there is space to interleave some instruction here). Good. The dot instruction can also be saving as it is often precomputed for other purpose.
Fresnel term
is a microfacet BRDF with a
term. Tri-ace give an efficient optimization for the three Fresnel term involve in the bottom layer.
The top water layer require the computation of , so
is available. The bottom layer need to compute
. The input of this two bottom Fresnel term is V’H (or V’H’). Graphing Fresnel terms from top (red) and bottom layer (blue) show the result present by Yoshiharu Gotanda (For IOR n1 = 1 the air, n2 = 1.33 the water and n3 = 1.55 the standard for dielectric material) :
Note that’s the blue line represent only . There is an important thing here. To do the previous graph, we need to use the full Fresnel equation. The Schlick approximation of Fresnel equation don’t handle total internal reflection which occur for
. Here is a compare of Fresnel equation (blue) and Schlick Fresnel (Red) for air-water interface (left) and water-air interface (right):
Tri-Ace purpose to approximate the almost flat line of bottom Fresnel terms by
Here, is the Fresnel equation for the normal direction. This gives us:
Comparing the approximation (red) with the original (blue) give :
Now applying the on the previous result and so getting the 3 terms Fresnel equation
(blue) and approximation
(red) :
Pretty good.
As we want to have thin layer on top of metallic material too, let’s extend Tri-Ace work with complex IOR (Metal unlike dielectric material have complex IOR varying with wavelength). A Fresnel bottom equation for metal could be writing:
Note that’s the formulation for for the complex IOR with complex number you may have seen (I use it before) give exactly the same result.
Using the full Fresnel conductor we graph the same 2 bottom terms as before but for aluminum instead (IOR n1 = 1 the air, n2= 1.33 the water, n3 = 1.65 k3 = 9.22 the red channel of aluminum). Approximation (blue) and original (Red):
 This time, it seems that’s the approximation is not good. However, graphing the full 3 terms
This time, it seems that’s the approximation is not good. However, graphing the full 3 terms (blue) and approximation
(red) :
 In fact the final result is good enough. This work for all values of n and k (like k = 0) and so is a generalized version of the one provided by Gotanda. The graph shows an interesting thing. Let’s add the air-metal interface Fresnel term of the red channel of aluminum on it (yellow) on the left figure. Then add the Fresnel term of the top layer (green) on the right figure:
In fact the final result is good enough. This work for all values of n and k (like k = 0) and so is a generalized version of the one provided by Gotanda. The graph shows an interesting thing. Let’s add the air-metal interface Fresnel term of the red channel of aluminum on it (yellow) on the left figure. Then add the Fresnel term of the top layer (green) on the right figure:
 The graph highlight that’s metal under a thin layer of water loss a little of specular reflection, which is exactly what we see on the copper ground example. At grazing angle, the Fresnel effect of the thin water layer will reflect all the light and the underlaying metal reflection down to 0%.
The graph highlight that’s metal under a thin layer of water loss a little of specular reflection, which is exactly what we see on the copper ground example. At grazing angle, the Fresnel effect of the thin water layer will reflect all the light and the underlaying metal reflection down to 0%.
The optimization presented here are important because they allow avoiding the requirement of the full Fresnel equation to handle the total internal reflection which can’t be handled by the Fresnel Schlick approximation.
Absorption term
I haven’t done any optimization work on this term. In fact as explain when introducing the double layer BRDF model, the absorption of water is negligible for such a thin layer so we can just remove it. But let’s analyze the TriAce optimization.
Tri-ace purpose to approximate with:
is simply the merge of
and
with some adjustment. I suppose the adjustment is done to better fit the original absorption term but it has not been discuss by Tri-Ace.
Let’s do a comparison, I graph for all angle with left an
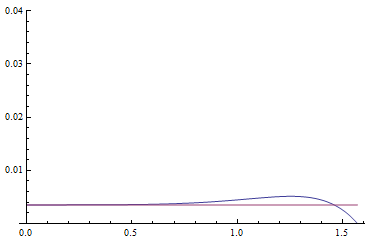
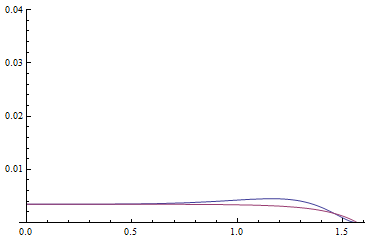
of 0.3 and right a value of 0.84. In both case the IOR of water 1.33 is use (also this has no impact for TriAce case). Bottom graph are the TriAce approximation, Up is the original term:
The results are rather good and taking into account that’s absorption coefficient is often chromatic, this is a good win on the exponential. As a remark, the above diagrams use the half vector H to refract the vector. Using N instead of H provide the result below. Which are rather poor. So be sure to follow [21] source code if you use TriAce optimization.
Final though
We see some potential optimizations for the double layer BRDF some from Tri-Ace and some based on the thin layer of water assumption. But there still plenty of inconvenient that’s in my opinion forbid the use of this model for game (At least for PS3/XBOX360).
One drawback is the need of IOR values everywhere. In game we mostly use specular parameters which represent Fresnel equation value at normal incidence. But this specular is calculated for air-surface interface at normal incidence with the equation . The normal incidence for the water-surface interface we need is
. Which mean we need to store a second specular color, (something we absolutely don’t want) or retrieve original IOR value from specular (which is not really possible with complex IOR for metal) at the cost of some instructions. And I know my artists will hate me if they need to manipulate complex IOR, think about Copper and its unintuitive parameters values: 3 n and 3 k…
Another problem I met is for the optimization with the FBottom term of TriAce. For performance I consider the surface BRDF as only one layer which include diffuse and specular. But to best fit in Weidlich and Wilkie layered model I should use 3 layers, one for the water, one for the specular and one for the diffuse.The consequence is that’s Fr2 include the diffuse term.
float3 Fr2 = BaseDiffuse + F23 * ((SpecPower + 2.0) / 8.0) *
pow(dotNH2, SpecPower);
float3 Fr = Fr1 + T12 * Fr2 * Absorption * T21;
float3 FinalColor = LightIntensity * (Fr) * dotNL1 + Env1 +
Env2 * T12 * Absorption * T21;
If I apply the FBottom optimization, I should have :
// With Fr2 not including the F23 as it is include in FBottom. float3 Fr = Fr1 + T12 * Fr2 * Absorption * FBottom;
That’s mean we will apply the Fresnel term to diffuse…
Another thing. To be able to do the transition between dry and wet material dynamically, we need to be clever. A lerp between the two models is costly. Using an IOR of 1, so having a air-air interface avoid to do the optimization based on the knowledge of the IOR of water (like refract). So it seems that’s a cheap solution is not so easy to find .
To conclude, despite its apparent simplicity our double layer BRDF even optimized is costly and not really artists friendly, especially for metal. We need a simpler way to deal with wet surfaces if we want our game to run well. Moreover, we have checked that’s this model is not sufficient to get the apperance of wet surfaces we are looking for. But the work done here is not useless, we have seen some interesting behavior and this will inspire less complex model.
Here are the Mathematica files corresponding to the graph of this section, one pdf: WeidlichWilkie and the notebook : WeidlichWilkie_nb (Right click, save, rename “.pdf” to “.nb” as wordpress don’t support zip files).
Added note:
According to [20], the effect of total internal reflection term is negligible:
The effect is almost negligible for surfaces with a low indices of refraction since t takes values on between 0.95 and 1. However, for a high IOR, the effect becomes a little bit more prominent, albeit still in a rather subtle fashion.
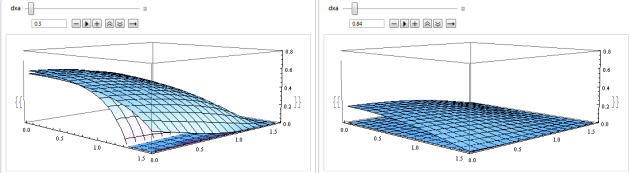
I wanted to check that’s total internal reflection term are negligible as stated by the authors. I graph the value of
in Mathematica based on the code provide in [21]. Left is
value for different L and V direction at N = 1.33 and Right is at N = 1.8:
I also plot a vector configuration with the light L and the view V (which are and
in equation above), the refracted light L’, the refracted view V’ and the half angle H. The value in {} from left to right are the angle in radian between V’ and H, value of G, value of Fresnel from water to air
and value of
.
As see in theory section, the critical angle of interface water-air is . The vector configuration show that’s when V.H is maximun, V’.H is also maximum because it is equal to the critical angle which give a value of 1 for Fresnel term. This is why on the
3D graph we have a decrease at grazing angle. So
is not negligible at grazing angle when Fresnel term is maximum.
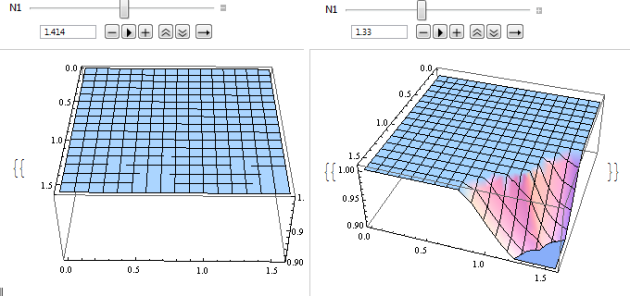
On this topic, there is a conference [10] claiming that’s is not noticeable at all for IOR > 1.41 and
. In fact, coming back to our story of using H or N to refract the vector, the author of [10] have use the N vector for his result. Here is a graph of
with vector refract with normal N:
[12] has an interesting insight about GPU implementation
Another consequence of the inability to actually sample the BRDF is that a discrepancy between the roughness of the layers might cause an incorrect appearance of the surface, specifically when m1 > m2. Figure 2 depicts the problem. This cannot happen in Monte-Carlo rendering, because the light gets properly blurred during the refraction on the upper layer. The solution here is to clamp the value of m2 to the value of m1 (see Line 21), so that the lower layer’s roughness is always greater or equal to the one of the upper layer.
Real time porous material
Pores/holes/cracks are at the origin of the second optical phenomena we study. This section will have a more in depth look at what is a porous material which is a required step to understand the interaction of porous material with water. In the theory section, we refer to rough or porous terms equally whereas roughness and porosity should be considered as two invisible micro-geometric features. Roughness is nearly always present on natural surfaces and has been well studied. But according to the fabrication process of objects considered, porosity is also often involved. In fact, nearly all of the materials that are naturally or industrially produced from powders are porous. Porosity is almost not considered in computer graphic, most BRDF use only a roughness parameter. However it has been show in material science that’s porosity can modify significantly the optical properties of surfaces. Porosity has also a large influence when considering changing appearance due to time: Dirt, Corrosion, efflorescence, pollution, tarnishing… And of course it has impact on appearances of wet surfaces as we already see.
The following figure highlight the difference between rough and porous micro-geometric features. It also show many kind of pores:
Porosity deserves some insight. There is currently few works on porosity in computer graphics: Mérillou and al [14] have purpose an analytic BRDF integrating porosity and this model have been extended to wet surface by Hnat and al [9][15]. All the content of this section are based on their works. Mérillou and al [14] note that the effect of pores can be viewed as modifying the diffuse and specular coefficients for any BRDF modeled as a microfacet distribution. They purpose a postprocess step on any BRDF which could be write as to integrate porosity on rendered surfaces. The principle behind this model is that incident light contribution to specular reflection is replaced by contribution to diffuse reflection and the contribution of incident light to diffuse reflection is modulated by total energy loss due to light interacting with pores.
In each case, the shadowing and masking effect of microfacet are take into account (The reader should refer to the paper [14] ( or [9]) for a detailed explanation). The new BRDF is written as:
with:
is the open porosity (also call effective porosity which are the pore of type b and c of the introducing figure, see [16] for a definition), closed porosity (which could matter for subsurface scattering of transparent material) are not considered
is the shadowing and masking term of pores. Even if any G term can be use, the author chose to use the Schlick optimization formulation of the model provided by Smith a G which takes into account the roughness to be more physically correct. This formulation is efficient to compute:
.
is the RMS slope of the microfacet.
represents the total light loss in the pore. The pores are supposed to be deformed cylindrical shape and light entering in it can bounces multiple time before exiting. Each bounce causes some light to be absorbed. The authors have done a simulation on lot of different pores shapes to estimate the average number of bounce incident light can do:
number of bounce and
is the ratio between mean depth of the pores and their average diameter. The more S_p is high, the deeper are the pores and so the more bounces we get.
may be written as
with
Note that [9] has some typo mistake and miss a power in which are corrected here. Here is a sample result from [14]:
Comparison between (a) a real world pot, (b) a dense pot, and (c) a porous pot.
Source [14]
The surface micro-geometry is characterized by roughness, open porosity and Sp. I implemented this BRDF for a simple Blinn-Phong model with the Disney BRDF explorer [17]. BRDF is a very well written tools to visualize/compare BRDF, binaries are available in the “Get started” part of [17] and the Porous BRDF can be get here PorousPostprocessBRDF (WordPress don’t support text files, so you must right click on the file, save it, rename it from “.pdf” to “.brdf” put the file in the “brdfs” directory of the BRDF explorer). If you just want to take a look at the code, the file can be read in a text editor.
The polar plot of BRDF explorer below, with left non porous BRDF and right porous BRDF, allow to see that’s the porous BRDF is a scaled version of the non porous BRDF (As claim by the authors). The behavior is approximately the same for all incident angle. The spheres show the visual result: A reduced diffuse and specular reflection:
Porosity = 0.35, Sp = 2, Kd = 0.7, Ks = 0.05, m = 0.19, indicent angle of 45°
The previous BRDF deal with porous material, Hnat and al. in [9] and Hnat thesis [15] have extended this BRDF for handling wet surface (and also pollution) for porous surface. They classify the porous BRDF in porous and non porous part:
| Material part | Diffuse part | Specular part |
|---|---|---|
| Non Porous | ||
| Porous |
Note that’s the terms has been rearranged compare to the previous formulation. They observe that’s non porous part of the material does not change with water interaction. The porous part is progressively filled with water replacing the porous diffuse reflection of the surface by a specular reflection due to water almost mirror-like.
That’s mean that’s the handling of wet surface is simply a linear interpolation between Diffuse porous part and water specular.
Note the porosity and shadowing and masking term include with the specular water representing the porous part. This effectively darkens the surface and increases the specular. This model doesn’t take into account the influence of a thin layer of water on the top of the surface.
The current formulation give in the paper deserve some simplification that’s the authors haven’t perform for the sake of clarity. Here is update and simplification of the previous BRDF which start from another formulation of this same BRDF in [14]:
The term can be simplifying to
, then using
we can replace the
in the above expression by:
For those not familiar with , it can be get from the specular power
and we can have
. A simple mad and rsqrt.
Thus we can write the wet porous surfaces BRDF for a Blinn-Phong BRDF as:
// Convert from roughness to specular power (beckmann style)
float SpecPower = 2 / (m * m) - 2;
float ks = Specular;
float kd = Diffuse;
float k = 1.0 / sqrt(SpecPower * PI / 4.0 + PI / 2.0);
float Gp = ( NdotV * NdotL ) / ( (NdotV- k * NdotV + k) *
( NdotL - k * NdotL + k ) );
float temp = ((acos(k1) * acos(k2)) / 2.0) - (2.0 * PI) / (Sp + 6.0);
float nb = Sp * ( 3.7 - 2.0 * temp * temp );
// No porous part
float alphaGp = Porosity * Gp;
float ksporo = ks * ( 1.0 - alphaGp );
float kdporo = kd * ( 1.0 - alphaGp );
float spec = ((SpecPower + 2.0) / (2.0 * PI)) * pow(NdotH, SpecPower);
float SpecPowerWater = 200.0;
float spec_water = ((SpecPowerWater + 2.0) / (2.0 * PI)) *
pow(NdotH, SpecPowerWater) * WaterSpecular;
// Wet porous part
float kwet = mix(alphaGp * pow((kd + ks), nb + 1) / PI, spec_water * alphaGp,
PoreFillingPercentage);
return vec3(kdporo / PI + ksporo * spec + kwet);
The Disney BRDF explorer file is here : WetPorousPostprocessBRDF. I use a direct specular water Blinn-Phong here instead of the indirect specular cubemap of the code provide in the thesis. The figure below show spheres: from left to right Porosity of 0, 0.1, 0.2, 0.3 ; Top dry and bottom fully wet.
 Sp = 1.3, Kd = 0.7, Ks = 0.05, Kwater = 0.02, m = 0.19, indicent angle of 21°
Sp = 1.3, Kd = 0.7, Ks = 0.05, Kwater = 0.02, m = 0.19, indicent angle of 21°
The polar plot shows the decrease in diffuse and increase in specular when wet but the visual result is subtle. On my test, the result depends a lot on low value of Sp parameters. Note that the first sphere of both row are the same, non porous objects have no inside water filling.
I have tested this wet porous BRDF and here are some thoughts :
The formulation of and
are a bit “old” and should be convert to “modern” energy conserving term.
should be a Specular Fresnel term and
the remaining diffuse. Moreover, the implementation code provided in the thesis seems to have a lot of independent parameter. For example the roughness and specular power of the Blinn-Phong model are not linked, the
term is not linked to any
implicit
term of Blinn-Phong. In practice, for game with a right formed BRDF, a microfacet with a
term derive from
and taken into account roughness, everything will be link. The
term will be the same as
, the roughness will be use both for
and as input for
etc… Despite the fact that this model has been proven to be able to represent real world material, in my test I haven’t get any satisfying result. The wetting process is barely visible because the contribution of the porous diffuse part is too small when
is > 2. I attribute all this to the input I provide but this is annoying.
Still that’s this wet BRDF has two major drawbacks. The calculus of nb is way too expensive for a game and the two extra parameters and
have no easy reference, a major problem for artists. Ideally a porous BRDF should have a simple parameter porosity
, the parameter
here is not intuitive for artists, and worth, it is not provided under this form by material science resource. In fact, these parameters have been chosen because they are easy to acquire from measurement in laboratory [18] and to the knowledge of the author, there is no relationship between
and
, so the porous BRDF can’t be reduce to one parameter.
For open porosity (or effective porosity) there is no good reference for it because it varies a lot even within a material and resource tends to provide range. The only resource I find is : http://web.ead.anl.gov/resrad/datacoll/porosity.htm.
[14] give example of open porosity for ceramic tiles 35%, concrete pot 25%, rocks such as limestone to 30-45% and sand to 25%. [15] give clay to 40-50% and chalk to 30-40%. But you can found different range depends on the sources.0
So, am I saying that’s all this section is useless ? Nope, porous and wet porous BRDFs are worth to look at because they have been able to simulate real world case. We just need to understand the principle of their construct and reuse idea. We will see that’s in the next section. And the main point, we learn about porosity which in involve in numerous aging and weathering effects.
Added note:
The wet porous BRDF do not consider the thin water layer that can be present on top of the material, but it can be enhance with a thin layer based on the double layer model presented in previous section.
These real time BRDF do not consider global illumination effect (like those from image based lighting), only a direct analytic formulation is provide. So additional research need to be performed to handle indirect lighting.
As porosity feature is a static state (i.e an objects don’t become dynamically porous, it is porous or not) and as it is a simple scaling of diffuse and specular coefficient, an artist could get a result close to real porous material with some tweaking (In fact this depend a little on the angle of incidence). I think this is one reason of the non adoption of porosity parameter (in addition of not being really artists friendly) by the graphic community. But depends on effects you need to handle in your game (dynamic weather, dynamic aging…) you may want to have a porosity parameter.
Approximation for game
We see two real time BRDF which simulate both optical phenomena involve with wet surfaces, they still however too expensive and not adapted for game. In the B part of this post, we will see other ways inspired by these one to simulate wet surfaces: Water drop 3b – Physically based wet surfaces.
Reference
[1] Wikipedia, “Total internal reflection”, http://en.wikipedia.org/wiki/Total_internal_reflection
[2] Jensen, Legakis, Dorsey, “Rendering of Wet Materials”, http://graphics.cs.yale.edu/julie/pubs/Wet.pdf
[3] Angstrom, “The Albedo of Various Surfaces of Ground”, Geogr. Ann.
[4] Twomey, Bohren, Mergenthaler, “Reflectance and albedo differences between wet and dry surfaces”, Applied Optics
[5] Hobbs, “Darker when wet”, http://www.abc.net.au/science/articles/2010/11/11/3063513.htm
[6] Gotanda, “Beyond a Simple Physically Based Blinn-Phong Model in Real-Time”, http://research.tri-ace.com/
[7] Lekner, Dorf, “Why some things are darker when wet”, https://www.victoria.ac.nz/scps/about/staff/pdf/darkerwhenwet.pdf
[8] Mall, Lobo, “Determining wet surfaces from dry”, http://www.vision.eecs.ucf.edu/papers/wet_dry_iccv.pdf
[9] Hnat, Porquet, Merillou, Ghazanfarpour, “Real-time Wetting of Porous Media”, http://damien.porquet.free.fr/msi/iccvg06/iccvg06.pdf
[10] Lee, “Modeling and Rendering of rendered materials”, http://www.slideshare.net/joohaeng/gw2-l-scce2010gist
[11] Lu, Georghiades, Rushmeier, Dorsey, Xu, “Synthesis of Material Drying History: Phenomenon Modeling, Transferring and Rendering”, http://graphics.cs.yale.edu/julie/pubs/Drying.pdf
[12] Elek, “Layered Materials in Real-Time Rendering”, http://www.cescg.org/CESCG-2010/sites/ElekOskar/
[13] Dorsey, Rushmeier, Sillion, Digital Modeling of Material Appearance book
[14] Mérillou, Dischler, Ghazanfarpour, “A BRDF Postprocess to integrate Porosity on Rendered Surfaces”, http://researchr.org/publication/MerillouDG00
[15] Hnat, thesis “Influence of surfaces micro-geometry on realistic rendering” in French, http://epublications.unilim.fr/theses/index.php?id=4820
[16] http://en.wikipedia.org/wiki/Porosity
[17] BRDF Explorer, http://www.disneyanimation.com/technology/brdf.html
[18] Personal communication with Stéphane Mérillou
[19] Weidlich, Wilkie, “Arbitrarily Layered Micro-Facet Surfaces”, http://www.cg.tuwien.ac.at/research/publications/2007/weidlich_2007_almfs/
[20] Weidlich, Wilkie, “Exploring the Potential of Layered BRDF Models”, http://www.cg.tuwien.ac.at/research/publications/2009/weidlich_2009_EPLBM/
[21] Weidlich, Wilkie, “Thinking in Layers – Modelling with Layered Surfaces”, http://www.siggraph.org/asia2011/courses-detail?id=100-6&session=Courses
[22] Pope, Fry, “Absorption spectrum ~380 –700 nm! of pure water. II. Integrating cavity measurements”, http://www.opticsinfobase.org/ao/abstract.cfm?uri=ao-36-33-8710
[23] universitetet i oslo, “Porous Material”, http://www.uio.no/studier/emner/matnat/kjemi/KJM5100/h06/undervisningsmateriale/16KJM5100_2006_porous_e.pdf


















Wow, thanks for sharing this. That’s an insane amount of work to put it in a post!
V1.1 :
I rewrite some part of Realtime double layer material section concerning the Absorption coefficient of water.In fact in the first version I put a single monochromatic absorption coefficient (based only on the red component) which is wrong.
The new version give right chromatic water absorption coefficient and is more verbose on this part. Unit, impact, the fact that’s for thin layer of water the influence is negligible etc… I also redo the ground screenshot of the RenderMonley application and submit a second version of it including the right absorption coefficient.
V1.2 : Add a nice figure to the real time porous BRDF section showing different shape of pores and highliting the difference between rough and porous micro-geometric features.
Hi Sebasten I have the same problem as you here
Specular maps of objects are usually modeled when viewed in air.
However when the objects are put underwater, the specular color should then be modified to reflect the different between refractive indices of water and material. Essentially, if the original specular color was identical to that of water, then the specular color as seen under water should vanish.
I think some approximation formula can do the trick but I have yet to find a good one.
Hey Christian,
if you can afford the extra instructions, you can simply get the IOR from specular color with n = (1 + sqrt(R0)) / (1 – sqrt(R0)). In this case you can handle dielectric material with water. The true problem come from Metal with their complex IOR which can’t be retrieve from specular color as there is several solutions.
V1.3 : Update Realtime double layer material section. The FresnelConductor formula take from Weidlich and Wiklie was wrong. I rewrite the code, update the RenderMonkey double layer application and redo the screenshots.
Pingback: Why do we look darker when we sweat? | fuckyeahphysica
hi sebastien
your blog help me a lot in my research on” wet and dark” for my final year project…….thanks so much
Pingback: Unreal Engine 4 – wet shader for all objects | Technical Graphic Director